Guayaquil, 6 de noviembre de 2015
Matemáticas 1
Puntos:
A: 0
B: 0
Ejercicio 1: En qué cuadrante se encuentran los siguientes puntos:
Puntos: (0, -1)
Ejercicio 6: Demostrar que los puntos: P1 (0, 1), P2 (3, 5), P3 (7, 2) y P4 (4, -2) son los vértices de un cuadrado.
Puntos:
P1 (0, 1)
P2 (3, 5)
P3 (7, 2)
P4 (4, -2)
Ejercicio 7: Determinar el punto medio de la recta comprendida entre el punto (3, 5) y el punto (7, 2).
Datos:
Puntos: (0, -1)
Ejercicio 2: En qué cuadrante se encuentran los siguientes puntos:
Puntos: (√2,π+3)
√2=1
π+3=6,14
Ejercicio 3: En qué cuadrante se encuentran los siguientes puntos:
Puntos: (-√8,π-5)
-√8=-2,82
π-5=-1,85
Ejercicio 4: En qué cuadrante se encuentran los siguientes puntos:
Puntos: (4+√5,-5+√2)
4+√5=6,24
-5+√2=-3,58
Ejercicio 5: Demostrar que los puntos: P1 (-2, -1), P2 (2, 2) y P3 (5, -2) son los vértices de un triángulo isósceles.
Puntos:
P1(-2, -1)
P2 (2, 2)
P3 (5, -2)
(P1P2) ̅= √[2-(-2)]〗^2+[2-(-1)]^2 (P1P2) ̅=√(4)^2+(3)^2
(P1P2) ̅=√16+9
(P1P2) ̅=√25=5
(P2P3) ̅=√(5-2)^2+(-2-2)^2
(P2P3) ̅=√(3)^2+(-4)^2
(P2P3) ̅=√9+16
(P2P3) ̅=√25=5
(P1P3) ̅= √[5-(-2)]〗^2+[-2-(-1)]^2 (P1P3) ̅=√(7)^2+(-1)^2
(P1P3) ̅=√49+1 (P1P3) ̅= √50=7,07
Puntos:
P1 (0, 1)
P2 (3, 5)
P3 (7, 2)
P4 (4, -2)
(P1P4) ̅=√4^2+3^2
(P1P4) ̅=√16+9
(P1P4) ̅=√25
(P1P4) ̅=5
(P2P3) ̅=√((7)-3)^2+(2-5)^2
(P2P3) ̅=√(4)^2+(-3)^2
(P2P3) ̅=√16+9
(P2P3) ̅=√25
(P2P3) ̅=5
(P4P3) ̅=√((7)-4^2+[2-(-2)]^2
(P4P3) ̅=√(3)^2+(〖4)〗^2
(P4P3) ̅=√9+16
(P4P3) ̅=√25
(P4P3) ̅=5
(P1P2) ̅=√((7)-4^2+[2-(-2)]^2
(P1P2) ̅=√(3)^2+(4)^2
(P1P2) ̅=√9+16
(P1P2) ̅=√25
(P1P2) ̅=5
Ejercicio 7: Determinar el punto medio de la recta comprendida entre el punto (3, 5) y el punto (7, 2).
Datos:
Puntos:
P1 (3, 5)
P2 (7, 2)
Proceso:
X ̅=(X1+X2)/2=(3+5)/2=8/2=4
Y ̅=(Y1+Y2)/2=(7+2)/2=9/2=4.5
P ̅=(4,4.5)
Datos:
Puntos:
P1 (2, 5)
P2 (4, 2)
P3 (1, 1)
Guayaquil, 9 de Noviembre de 2015
Ecuación de la recta que pasa por 2 puntos
Geométricamente queda perfectamente determinada por 2 cualesquiera de sus puntos, analíticamente la ecuación de una recta también queda perfectamente determinada conociendo las coordenadas de 2 cualesquiera de sus puntos.
Ejercicio 1: Hallar la ecuación de la recta que pasa por los 2 puntos:
A (4, 2) y B (-5, 7).
Ecuación Simétrica de la Recta
Ejercicio 2: Los segmentos que una recta determina sobre los ejes x y y son 2, -3 respectivamente. Hallar su ecuación:
Ejercicio 3: Una recta pasa por los 2 puntos A (-3,-1) y B (2,-6). Hallar su ecuación en la forma simétrica.
Forma general de la ecuación de una recta
Ejercicio: Hallar los valores que deben tener los coeficientes de la ecuación general Ax+By+C=0 para que pase por los 2 puntos: P1 (-1, 4) y P2 (3, -2). Hallar la ecuación de la recta.
Puntos:
P1 (-1, 4)
P2 (3, -2)
Ax+By+C=0
P1 (2, 5)
P2 (4, 2)
P3 (1, 1)
Proceso:
X ̅=(x_1+x_2)/2
2=(x_1+x_2)/2
4=x_1+x_2
y ̅=(x_2+y_2)/2
5=(x_2+y_2)/2
10=x_2+y_2
4+0+y_3= 2 y_2= 4+2
y_3= -2 y_2= 6
Pendiente
Puntos:
P1 (3, 3)
P2 (1, 3)
m=0
x_1=3
x_2=1
y_1=3
y_2=3 m= (Y2-Y1)/(X2-X1)= (3-3)/(1-3)= 0/(-2)= 0
Ejercicio 9: h(x)= bx/2
h (x)= bx/2
m= b/2
Ejercicio 10: Ax+By+C=0 y=?
By= -Ax-C
y= (-Ax-C)/B
y= (-Ax)/B-C/B
m=-A/B
2x+3y+5=0
m= -2/5
b= -5/3
Ejercicio 11: Hallar la ecuación de la recta que pasa por el punto A (1, 5) y tiene de pendiente 2.
Punto (1, 5)
m= 2
Ec. de la recta: Ax+By+C=0
m=(Y2-Y1)/(X2-X1)
2=(5-Y)/(1-X)
2(1-x)=5-Y
2-2X=5-Y
2X-Y+3=0
Ejercicio 12: Hallar la ecuación de la recta que pasa por el punto A (-6, 3) y tiene un ángulo de inclinación de 45°.
Datos:
Punto: A (-6, 3)
45°
1=(Y+3)/(X+6)
Tang 45°= op/ady=1/1=1 X+6=Y+3
m=1 X-Y+3=0
2X-Y+3=0
Guayaquil, 9 de Noviembre de 2015
Matemáticas 1
Ecuación de la recta que pasa por 2 puntos
Geométricamente queda perfectamente determinada por 2 cualesquiera de sus puntos, analíticamente la ecuación de una recta también queda perfectamente determinada conociendo las coordenadas de 2 cualesquiera de sus puntos.
Ejercicio 1: Hallar la ecuación de la recta que pasa por los 2 puntos:
A (4, 2) y B (-5, 7).
Ax+By+C=0
(y-y_1)= (y^2-y^1)/(x_2-x_1 )(x-x_1)
y-2=(7-2)/(-5-4)(x-4)
y-2= (-5)/9(x-4)
9 (y−2)= -5 (x-4) 9(y-7)= 5(x-5)
9y−18= -5x+20 9y-63=5x-25
5x+9y−38=0 9y-63+25=5x
9y-38-5x= 5x+9y-38
Ejercicio 2: Los vértices de un cuadrilátero son: A (0, 0), B (2, 4), C (6, 7) y D (8, 0). Hallar la ecuación de sus lados.
Ax+By+C=0
A (0, 0) y B (2, 4)
(y-y_1)= (y^2-y^1)/(x_2-x_1 )(x-x_1)
y= 4/2
y= 2x
2x-y= 0
B (2, 4) y C (6, 7)
(y-y_1)= (y^2-y^1)/(x_2-x_1 )(x-x_1)
y-4= (7-4)/(6-2) (x-2)
y-4= 3/4(x-2)
4(y-4)= 3(x-2)
4y-16= 3x-6
-3x+4y= -6+16
3x-4y= -6+16
3x-4y+10= 0
C (6, 7) y D (8, 0)
(y-y_1)= (y^2-y^1)/(x_2-x_1 )(x-x_1)
y-7= (0-7)/(8-6) (x-6)
y-7= (-7)/2 (x-6)
2(y-7)=-7(x-6)
2y-14= -7x+42
7x+2y-46= 0
Ejercicio 1: Sea A ≠0 B≠0 los segmentos de una recta determinada sobre los ejes x y y, es decir sus intercepciones, hallar la ecuación de la recta que pasa por los 2 puntos.
y-y1 =y2-y1/x2-x1. (x-x1)
y-0= b-0 /0-a. (b-o)/(0-a). (x-a)
y=-b/a. (x-a)
ay=-bx+ab
bx/ab+ay /ab=ab/ab=x/a+y/b=1
Ejercicio 2: Los segmentos que una recta determina sobre los ejes x y y son 2, -3 respectivamente. Hallar su ecuación:
x/2-y/3= 1
Ax+By+C= 0
3x-2y-6= 0
x/2-y/3= 3x-2y/6
3x-2y/6= 1
3x-2y= 6
3x-2y-6= 0
X1, Y1
A (-3,-1)
B (2, -6)
X2, y2
y-y1= y2-y1/x2-x1.(x-x1) y+1= -6+1/2+3.(x-x1)
y+6= -6+1/2+3.(x-2) y+1= -5/5.(x+3)
y+6= -1(x-2) y+1= -1(x+3)
y+6= 2-x y+1= -x-3
x+y+4= 0 x+y+4= 0
x+y= -4
-x/4-1/4= 1
Ejercicio 4: Una recta de pendiente -3 pasa por el punto A (-1, 4). Hallar su ecuación en la forma simétrica.
Pendiente
m= -3
y-1= m(x-x1)
y-4= -3(x-(1))
y-4= -3x-3
3x+y= 1
x/(1⁄3)+y/1= 1 a=1/3 b=1
x/1.3/1= 3x
5x+2y=1
x/(1⁄5)+y/(1⁄2)=1
a=1/5 b=1/2
Ejercicio 5: Hallar la ecuación de la recta que pasa por el punto A (-2, 4) y determina sobre el eje x el segmento -9.
X segmento9= x_1 y_2 x_2 y_2
(-2, 4) (-9, 0)
y-y_1= y2-y1/x2-x1.(x-x_1)
y-4= 0-4/-9+2.(x+2)
y-4= -4/-7.(x+2)
-7(y-4)= -4(x+2)
-7y+4= -4x-8
-7y+28= -4x-8
4x-7y+36=0
Ejercicio 6: Hallar el área del triángulo rectángulo formado por los ejes coordenados y la recta cuya ecuación es 5x+4y+20=0.
Ec. simétrica:
5x/(-20)+4y/(-20)=(-20)/(-20) A∆=(-4)(-5)/2=10u^2
x/(-4)+y/(-5)=1
(-4, -5)
Forma general de la ecuación de una recta
Ejercicio: Hallar los valores que deben tener los coeficientes de la ecuación general Ax+By+C=0 para que pase por los 2 puntos: P1 (-1, 4) y P2 (3, -2). Hallar la ecuación de la recta.
Puntos:
P1 (-1, 4)
P2 (3, -2)
Ax+By+C=0
A (3)+B (-2)+C=0
(-3/5 C)x+(-2/5 C)y+C=0
-5(-3cx/5-2cy/5+c)
3cx+2cy-5c=0
Factor común c=(3x+2y-5)=0
3x+2y-5=0
S
Sistema de ecuaciones:
-A+4B+C=0
-A+4(2C/5)+C=0
-A-8C/5+C=0
-A-3C/5=0
-A+3/5 C=0
A=-3/5 C
Guayaquil, 16 de Noviembre del 2015
Matemáticas 1
Ejercicios en clase
Ejercicio 1: Hallar el valor de K para que la recta Kx + (K-1)y-18=0 sea paralela a la recta 4x+3y+7=0.
Kx+ (K-1)y-18=0
4x+3y+7=0
4x+3y= -7
4x/(-7)+3y/(-7)= (-7)/(-7)
x/((-7)⁄4)+y/((-7)⁄3)= -1
a= (-7)/4= -1.75
b= (-7)/3= -2.33
m= -A/B
m= -4/3
m=K/(K-1)
m1= m2
(-4)/3=(-K)/(K-1)
-4(K-1)=3(-K)
-4K+4=3K
3K+4K=4
7K=4
K=4
4x/7.(4/7-1)y-18=0
4x+3y-18=0
Ejercicio 2: Determinar el valor de K para que la recta K^2 x+(K+1)y+3=0 sea perpendicular a la recta 3x-2y-11=0.
K^2 x+(K+1)y+3=0
3x-2y-11=0
3x-2y=11
x/(11⁄3)-y/((-11)⁄2)= 11/11
a= 11/3=3.66
b= 11/2= -5.5
m1.m2= -1
m1= 3/2
-2=K -2=-3K+2
-4= -3K
4/3=K
-2=-3K^2+2
K= (2±2√7)/(2(3))
K= ((1±√7))/3
K_1=(1+√7)/3 K_2=(1-√7)/3
Punto: (2, 3)
2x-7y+2= 0
2x-7y= -2
x/((-2)⁄2)-y/((-2)⁄7)=(-2)/(-2)
a=(-2)/2= -1
b=(-2)/7= 0,28
m_1= 2/7
m= tangӨ Ө=tang^(-1). m
Ө=tang^(-1). (2/7)
Ө= 15,94°
y-y_1= m_2(x-x_1)
y-3= -7/2.(x-2)
2y-6= -7x+14
7x+2y-20= 0
Matemáticas 1
Ejercicio 1: Demostrar que los ángulos suplementarios formado por Ax+By+c=0 está dado por la fórmula Tagϑ=(A'B-AB')/(BB'+AA')
Ax+By+C=0 m_1=-A/B
A’x+B’y+C’= 0 m_2=-A'/B'
Tagϑ=(Tagβ_2-Tagβ_1)/(1+Tagβ_1 (Tagβ_2 ) )
m_2=Tagβ m_1=Tagβ_1
Tagϑ=(m_2-m_1)/(1+m_2 (m_1 )
Tagϑ=(-A'/B'+A/B)/(1-A'/B'(-A/B) )
Tagϑ=(A'B-AB')/(B'B+AA')
Ejercicio 2: Distancia de una recta a un punto. La recta de la distancia del punto a la recta es perpendicular a la recta.
Ax+By+C=0
P(x_1,y_1 ) m_1=-A/B m_2=B/A
Ecuación punto-pentiente y-y_1=m(x-x_1 ) y-y_1=B/A (x-x_1 ) Ax-Ay_1=Bx-Bx_1
A^2/B x+Ay+AC/B= 0
Bx-Ay+Ay_1-Bx_1= 0
(Bx+A^2)/B+AC/B+Ay_1-Bx_1= 0
x((B^2+A^2)/B)= (B^2.x_1-AB.y_1AC)/B
x=(B^2.x_1-ABy_(1-AC))/(B^2+A^2)

Ejercicio 3: Hallar la distancia de la recta 4x-5y+10=0 al punto (2,-3)
4x-5y+10= 0 P (2,-3)
d=(l(Ax_1+By+C)l)/√(A^2+B^2 )
d=(l4(2)+(-5)(-3)+10l)/(4^2+5^2 )= (l8+15+10l)/√41= 33/√41
Ejercicio 4: Los vértices de un triángulo son: A (-4,1) B (-3-3) C (3,-3). Hallar la longitud de la altura del vértice A sobre el lado BC y el área del triángulo.
m=(y_2-y_1)/(x_2-x_1 )=(-3-3)/(3+3)= -1
y-y_1=m(x-x_1 )y-3= -1(x+3) x+y= 0
Ejercicio 5: La ecuación de una circunferencia es(x-4)^2+(y-3)^2=20. Hallar la ecuación de la tangente a éste círculo en el punto (6,7).
C (4,3) r=20
A(6)+2(A)+C= 20
√20(A√5)=l4A+6A+Cl
10A=10A+C
m= -1/2 P(6,7)
y-7=-1/2(x-6)
2y-14=-x+6
x+2y-20=0
Ejercicio 6: Forma general de la ecuación de la circunferencia.
x^2-2xh+h^2+y^2-2ky+k^2=r^2 (x-h)^2+(y-k)^2=r^2
Ax^2+By^2-2hx-2ky+h^2+k^2=r^2
A=B
-Recudir la siguiente ecuación a la forma ordinaria de la ecuación de la circunferencia.
2x^2+y^2-10x+6y-15= 0
x^2-5x+y^2+3y=15/2
(x^2-5x+25/4)+(y^2+3y+9/4)=15/2+25/4+9/4
(x-5/2)^2+(y+3/2)^2=16
Ejercicio 7: Reducir la siguiente ecuación a la forma ordinaria de la ecuación de la circunferencia.
36x^2+12y^2+48x-108y+970
No se puede porque A≠B
Guayaquil, 30 de Noviembre de 2015
Matemáticas 1
Parábola
Es un lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia de una recita fija situado en el plano, es siempre igual a su distancia de un punto fijo del plano y que no pertenece a la recta.
Al punto se lo llama foco.
La recta fija se llama directriz de la parábola.
Nota: Esta definición excluye el caso en que el foco está sobre la directriz.
En la gráfica se representa al foco con la letra F mayúscula.
A la directriz con la letra L minúscula, al vértice con la letra v.
V o vértice es el punto medio del segmento AF.
A es el punto de intersección del eje de la parábola y de la directriz.
La recta a minúscula que pasa por F y es perpendicular a L se llama eje de la parábola.
Cuerda focal: una cuerda que pasa por el foco se llama cuerda focal.
Cuando la cuerda focal es perpendicular a la recta se llama lado recto.
*Ecuación de la parábola de vértice en el origen y eje.
-La forma más simple para la ecuación de una parábola, es cuando su vértice está en el origen y su eje coincide con el eje x.
La definición de parábola es la siguiente:
-La distancia del foco al punto P debe ser igual a la distancia del punto P hacia la directriz.
X+F=0
Ejercicio 1: Determine la ecuación de la parábola si el vértice está en el origen y su eje coincide con el eje y.
P(x, y)
F (0,F)
√(x^2+(F-y)^2 )=√((x+F)^2 )
x+(F-y)^2= (x+F)^2
x^2+F^2-2Fy+y^2= x^2+2Fx+F^2
x=√4Fy
Las ecuaciones x^2=4Fy y y^2=4Fx se la suelen llamar la primera ecuación ordinaria de parábola.
P(x,y) F(3,0)
l+F=0 l-3
X+3=0
lPFl=√((3-x)^2+y^2 )
(x+3)^2=√((3-x)^2+y^2 )
12x=y^2
lPll=(lx(3)+0+3)/√(A^2+B^2)
lPll=x+3
Ejercicio 3: Hallar la ecuación de la parábola del v en el origen y F (0,-3).
L=x l+F=0
Y-3=0
lPFl= √(x^2+(y+3)^2 )
(y-3)^2= x^2+(y+3)^2
lPl=(l1(y)-3)/1= y-3
-6y-6y= x^2
x= √(-12y)
Ejercicio 4: Hallar la ecuación de la parábola del v(0,0) y directriz de la recta y-5=0.
L: y=5 v (0,0) F (0,-5)
lPll= (l1(y)-5l)/1= y+5
lPFl= √(x^2+(y+5)^2 )
(y-5)^2= x^2+y^2+10y+25
x^2= -20y
Ejercicio 5: Una cuerda de la parábola y^2-4x=0 es un segmento de la recta x-2y+3=0. Hallar su longitud.
x-2y+3= 0
y^2-4x= 0
x= -3+2y
y^2-4(-3+2y)= 0
y^2-8y+12=0 (y-2)(y-6)= 0
y_1= 2 y_2= 6
x= -3+2y
x= -3+2(2)
x_1= 1 x_2= 9
Guayaquil, 4 de Diciembre de 2015
Matemáticas 1
Ejercicio 1: Determinar la ecuación de la circunferencia que pasa por los vértices y los puntos extremos del lado recto de la parábola.
LR= 4p= 4(1)= 4 A (-2,1) B (2,1) F (0,1)
x^2-4y= 0
(x-h)^2+(y-k)^2= r^2
(-2-h)^2+(1-k)^2= r^2
(2-h)^2+(1-k)^2= r^2
(-2-h)^2= (2-h)^2 8h=0 h=0 h^2+k^2=r^2 k^2=r^2 k=r (2-0)^2+(1-r)^2=
r^2 r= 5/2 x^2+(y-5/2)^2= 5/2^2 x^2+y^2-5y= 0
x^2-4y= 0
(x-h)^2+(y-k)^2= r^2
(-2-h)^2+(1-k)^2= r^2
(2-h)^2+(1-k)^2= r^2
(-2-h)^2= (2-h)^2 8h=0 h=0 h^2+k^2=r^2 k^2=r^2 k=r (2-0)^2+(1-r)^2=
r^2 r= 5/2 x^2+(y-5/2)^2= 5/2^2 x^2+y^2-5y= 0
Ejercicio 2: Hallar la longitud de la cuerda focal de la parábola x^2+8y=0 que es paralela a la recta 3x+4y-7=0.
F (0,-2) m= -3/4
y+2= -3/4 (x-0) 3x+4y+8= 0
x^2+8y= 0
-6x-8y-16= 0
x^2-6x-16= 0
3x+4y+8=0 3(8)+4y=-8 y=-32/4 y_1=-8
3(-2)+4y=-8 y_2=-1/2
P_1 (8,-8) P_2 (-2,-1/2)
Ejercicio 3: En cada uno de los ejercicios hallar las coordenadas del F para la ecuación de la directriz y distancia del lado recto y discutir el lugar geométrico correspondiente.
a. y^2= 12x
Foco y^2=4Fx
12= 4F F= 3 F(0,3) Ec.directriz x+3= 0
Longitud del lado recto 4F= 12
b. y^2+8x= 0
Foco y^2= -8Fy F= -2 F(-2,0)Ec.directriz x-2= 0
Longitud de lado recto
l4Fl= -8 F= 2
c. x^2= 12y
Foco 4F=12 F= 3 F(0,3)
directris y+3= 0
Longitud de lado recto l4Fl=12 F= 3
d. x^2+2y= 0
Foco x^2= -2y 4F= -2 F= -1/2 F(0,-1/2)
directris y+F= 0 y-1/2= 0
Longitud del lado recto l4Fl= -2 F= 2/4 F= 1/2
Ejercicio 4: Hallar la ecuación de la parábola de vértice en el origen y F (3,0)
V (0,0) F (3,0) F= 3
(y-h)^2= 4F(x-k)
y^2= 12x
Guayaquil, 7 de Diciembre de 2015
Matemáticas 1
Ejercicios:
Ejercicio 1: Determinar la ecuación de la parábola que tiene su vértice en (h,k) y el eje del vértice es paralelo al eje coordenada de las x.
V (h,k) v(0,0)
X= x-h y=y-k
y^2=4Fx
(y-k)^2= 4F(x-h)
Ejercicio 2: Hallar la ecuación cuyo vértice es (-2,3) y el F (1,3). Hallar la ecuación de su directriz y la distancia de su lado recto.
V (-2, 3) F(1,3) x+5= 0
h+f= 1 -2+F= 1 F= 3
LR:l4Fl= 4(3)= 12
F(h+F,k)
(y-3)^2= 4(3)(x+2)
y^2-6y-12x-15= 0
Ejercicio 3: Hallar la ecuación de una parábola cuyo eje del vértice sea paralela al x, y que pase por los puntos (3,3) (6,5) (6,-3).
A (3,3)
(3-k)^2= 4F(3-h)
k^2-6k-12F-4Fh= -9
B(6,5) (5-k)^2= 4F(5-h) 25-10k+k^2= 24F-4Fh
C(6,-3) (-3-k)^2= 4F(3-h) 9+6k+k^2= 24F-4Fh
-9+6k-k^2=12F-4Fh
25-k+k^2=24F-4Fh
16-4k=12F
-25+10k-k^2=-24F+4Fh
9+6k+k^2=24F-4Fh
-16+16k=0 k=1
16-4k=12F
16-4(1)=12F
16-4=12F 12=12F F=12/12 F=1
9-6k+k^2=12F-4Fh
9-6+1=12-4h -8=-4h h=-8/(-4) h=2
(y-k)^2=4F(x-h)
(y-1)^2=4F(x-2)
y^2-2y-4x+9=0
Ejercicio 4: En cada uno de los ejercicios del 11 al 15 realizase la ecuación dada a la segunda forma ordinaria de la ecuación de la parábola y hallar las coordenadas del v y F, las ecuaciones de la directriz y eje, y la longitud del lado recto.
1. 4y^2-48x-20y=71
4(y-5/2)^2= 48(x+2)
(y-5/2)^2= 12(x+2) 4F= 12
F= 3
v(-2,5/2) lLRl= 12
directris x+7=0
2. 9x^2+24x+72y+16= 0
9(x+4/3)^2= -72y
(x+43)^2= -8y
F= -8/4 F= -2
V(-4/3,0)
directriz y+ F= 0 y-F= 0
3. 4x^2+48y+12x= 154
4(x^2+3/2)= 168-48y
(x+3/2)^2= 42-12y
(x+3/2)^2=-12(y-7/2)
4F= -12 F= -12/4 F= -3
LR= l4Fl LR= l4(-3)l= 12
v(-3/2,7/2)
directriz y-7= 0






























































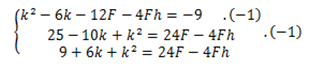




No hay comentarios:
Publicar un comentario