Universidad de Guayaquil
Facultad de Ingeniería Química
Carrera de Ingeniería Química
|
|
Nombre:
|
María Fernanda Díaz
|
Asignatura:
|
Matemáticas 1
|
Paralelo:
|
1er semestre B
|
Fecha:
|
26/02/2016
|
Docente:
|
Ing. Manuel Fiallos
|
Ejercicios en clase:
Determine si las siguientes funciones son crecientes o decrecientes.
y=3x+3
Al derivar la función
y=3x+3
y'=3
Determinamos que es creciente.
¿Cómo sabemos hacia qué lado es cóncava? Esto se explica con el teorema de concavidad, sacando la 2da derivada.
y'=3
y''=0
Si es 0, quiere decir que no es cóncava.
La segunda derivada de f(x) cuando es mayor a 0, la función es cóncava hacia arriba y si f(x) es menor a 0 entonces es cóncava hacia abajo
Ejemplo:
h(t)= t^2+2t-3
h(t)=(t+3)(t-1)
h(t)= t^2+2t+1-1-3
h(t)=(t+1)^2-4
Una vez hemos simplificado la función podemos derivarla
h^' (t)=2t+2
h^''(t)=2
H’’(t) es mayor a 0, por lo tanto es cóncava hacia arriba
Ahora determinamos los puntos críticos
h^' (t)=2t+2
0=2t+2
t=-1
Decreciente (-∞,-1)
Creciente (-1,∞)g(x)=2x^3-9x^2+12x
Primera derivada
g(x)=2x^3-9x^2+12x
g'(x)=6x^2-18x+12
Puntos críticos
0=6x^2-18x+12
0=(x-2)(x-1
x=2; x=1
Creciente (-∞,1)U (2,∞)Decreciente (1,2)
Segunda derivada
g'(x)=6x^2-18x+12
g^''(x) =12-18
f(x)=x^3-1
Primera derivada
f(x)=x^3-1
f'(x)=3x^2
Segunda derivada
f''(x)=6x
Nota: Toda la gráfica es creciente
Utilice el teorema de concavidad para determinar en donde la función dada es cóncava hacia arriba y cóncava hacia abajo además de los puntos de inflexión
f(x)=(x-1)^2
Derivamos
f(x)=(x-1)^2
f'(x)=2x-2
Puntos críticos
0=2x-2
x=1
Creciente (1,∞)
Decreciente (-∞,1)
Segunda derivada
f'(x)=2x-2
f''(x)=2
Es cóncava hacia arriba
T(t)= 3t^3-18t
Primera Derivada
T(t)= 3t^3-18t
T'(t)= 9t^2-18
Puntos críticos
0= 9t^2-18
t= ±√2
Creciente (-∞,-√2) U (√2,∞)
Decreciente (-√2,√2)
Segunda derivada
T'(t)= 9t^2-18
T''(t)= 18t
Ejercicios razón de cambio
Suponga que se vierte Agua en un depósito cónico a ½ pulgada^3/s, determine la altura en función de t y dibuje h(t) desde t=0. El diámetro es de 2 pulgadas y una altura de 4 pulgadas.
Vcono=1/3 πr^2 h
Vcono=1/3 π h/4^2 h
16Vcono=1/3 πh^3
Derivamos
16dv/dt=πh^2 dh/dt
16dv/dt=πh^2 dh/dt
Reemplazamos valores
16(1/2)=πh^2 dh/dt
8/(πh^2 )=dh/dt
Hallar una relación entre h con el tiempo
dv/dt=(1 inch^3)/2
(1 inch^3)/2 t=Volumen
√
Despejamos
Vcono=1/3 (πh^2)/16
1/2 t= (πh^2)/48 h
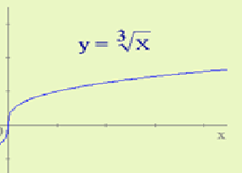
h(t)=∛(24t/π)
Primera derivada
Segunda derivada
La segunda derivada tiene signo negativo, por lo que su concavidad es hacia abajo








No hay comentarios:
Publicar un comentario